What Is A Parent Function?

Last Updated on November 16, 2023

A parent function is the most basic form of a mathematical equation or function that can be used as a template to create other similar functions. The parent function conveys the fundamental characteristics and behavior of all the related functions that can be derived from it.

In mathematics, parent functions are essential for graphing and understanding more complex functions. They provide a basis for exploring and visualizing the behavior of different types of functions. By studying parent functions, we can identify patterns and relationships between different functions.

Moreover, parent functions play a vital role in calculus, where they are used to help find the derivatives and integrals of more complex functions. In this article, we will explore some of the common types of parent functions, and how they can be used in different real-world situations.

Credit: www.thoughtco.com

What Are Parent Functions? An Introduction

Definition Of Parent Function

In mathematics, a parent function is a simple function that can be transformed into other functions of the same family by changing some parameters. In other words, it’s a fundamental function that serves as a template for related functions. The parent function is the unmodified form of a function and is usually the first function that students learn in their math classes. See here – why is math important?

Basic Characteristics And Properties Of Parent Functions

Parent functions have specific characteristics and properties that are essential to understanding them and their related functions. The following are some of the basic properties of parent functions:

Domain and range: Parent functions have a specific domain and range within which they operate and produce outputs. Understanding the domain and range of a function is crucial in determining its behavior.
Symmetry: Some parent functions have symmetry, which means that they have a mirror image. For example, the parent function y = x² is symmetric around the y-axis.
Intercept: The intercept is a point where the graph of a parent function intersects either the x-axis or the y-axis. The x-intercept is the point at which the graph intersects the x-axis, whereas the y-intercept is the point at which the graph intersects the y-axis.

Asymptotes: Some parent functions have asymptotes, which are imaginary lines that the graph approaches but never touches. The vertical asymptote occurs where the denominator of a fraction function equals zero.

Why Parent Functions Are Important In Mathematics

Parent functions are essential to understanding how related functions behave. By knowing the underlying structure of a parent function, we can apply the same logic and principles to entire families of related functions. This ability to transform parent functions ultimately allows us to solve more complex mathematical problems.

Moreover, parent functions are used as a tool to study the properties of other functions. They provide the basics that allow us to recognize similar patterns in related functions. By studying parent functions, students in math classes can develop a better understanding of functions in general and learn how to solve more complex problems using algebraic methods.

Understanding parent functions is crucial for students of mathematics. By learning about their characteristics and properties, we can recognize patterns in related functions and use them to solve more complex problems effectively. With a solid understanding of parent functions, math students can confidently tackle advanced mathematical concepts with ease.

Common Types Of Parent Functions

Common Types Of Parent Functions:

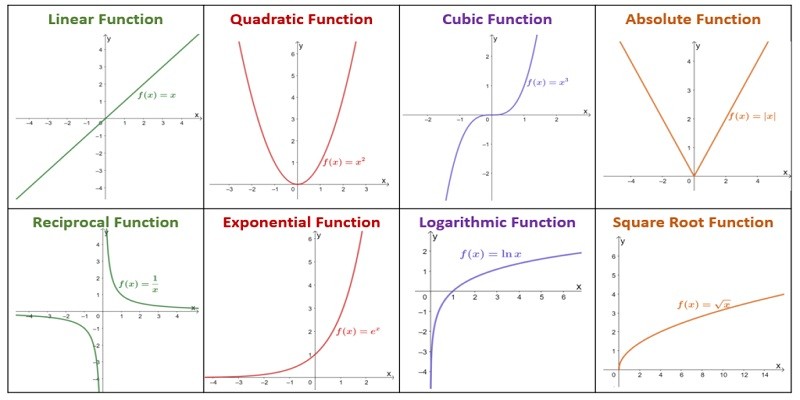
Parent functions are the most fundamental types of functions. They are simple functions that can be used to create more complex functions by changing their constants and coefficients. There are various types of parent functions, such as linear, quadratic, cubic, radical, exponential, and logarithmic functions.

Let’s take a closer look at each of them and understand what makes them unique.

Linear Parent Function: Y = X

The linear parent function is a straight line that passes through the origin (0,0) and has a slope of 1.
It is characterized by a constant rate of change.
The equation y = mx + b is used to represent a linear equation that is not the parent function. Here, m is the slope and b is the y-intercept.

Quadratic Parent Function: Y = X^2

The quadratic parent function is a parabola-shaped curve. It is a u-shaped curve that opens either upward or downward.
Its vertex is located at the origin (0,0), and it has a minimum or maximum value depending on the opening direction of the parabola.
It is characterized by a non-constant rate of change, where the slope of the curve changes as the value of x changes.

Cubic Parent Function: Y = X^3

The cubic parent function is a curve that resembles an elongated s-shape. It has an inflection point where the direction of the curve changes.
It passes through the origin (0,0), and its slope gradually increases or decreases as the value of x increases or decreases.
The cubic function is used to represent situations where the output value changes with the cube of the input value.

Radical Parent Function: Y = √X

The radical parent function is a curve that starts from the origin (0,0) and extends towards the right.
It has a limited domain, and the value inside the square root must be non-negative, otherwise, it will result in an imaginary number.
The curve is characterized by a slow rate of change near the origin (0,0), while it increases rapidly as x increases.

Exponential Parent Function: Y = E^X

The exponential function is a curve that increases rapidly as x increases. It is characterized by an exponential growth pattern.
The curve passes through the point (0,1), and its slope increases or decreases based on the value of x.
The exponential function is used to represent exponential growth or decay in various natural phenomena.

Logarithmic Parent Function: Y = Log(Base A) X

The logarithmic parent function is the inverse of the exponential function. It is a curve that starts from the y-axis and extends towards the right.
It has a limited domain, as the value of x inside the logarithm must be positive.
The logarithmic function is used to represent situations where the output value changes with the logarithm of the input value.

Understanding the different types of parent functions is crucial in mathematics. It helps to create complex functions that can be used to solve various real-world problems. These functions have unique characteristics that make them suitable for different situations. Knowing how to manipulate these functions is essential for success in any advanced mathematics course.

Domain And Range Of Parent Functions

A parent function is the most basic form of a mathematical function. It is a function that is not altered or transformed in any way. In this section, we will discuss the domain and range of parent functions.

The domain of a parent function is the set of all possible input values for which the function is defined.

The range of a parent function is the set of all possible output values that the function can produce.

For example, the domain of the parent function for a linear equation is all real numbers, whereas the range is also all real numbers. The parent function for an exponential equation has a domain of all real numbers and the range is greater than zero.

Understanding the domain and range is critical in limiting the solution set to the function.

Transformation Of The Parent Function

Transformation is a process of changing the shape, position or size of a parent function. In order to transform a parent function, we apply specific operations to the equation. Here are the main transformations that can be made to transform a parent function:

Vertical shift: This involves moving the graph of the parent function up or down. We simply add or subtract a value to the function.
Horizontal shift: This involves moving the graph of the parent function left or right. We simply add or subtract a value to the input variable in the equation.

Vertical stretch or compression: This change is made by multiplying the parent function by a constant value, causing the graph to stretch or compress vertically.

How To Graph Parent Functions

Graphing a parent function requires an understanding of domain, range, and how to apply the transformations discussed earlier. Here are some steps to follow when graphing a parent function:

Identify the parent function for the equation you want to graph.

Plot the points of the parent function on a coordinate plane.
Apply the transformation(s) to the parent function to create a new equation.
Use the new equation to plot the points of the transformed function on a coordinate plane.

Adjust the domain and range if necessary.
Trace the graph on the coordinate plane.

A parent function is a fundamental component of mathematical functions and understanding the concepts of the domain, range, transformation, and graphing is essential for any student of mathematics. Following the steps carefully will ensure that you understand each step of the process.

Frequently Asked Questions On What Is A Parent Function?

What Is A Parent Function?

A parent function is the simplest form of a set of functions with similar characteristics.

How Do You Identify A Parent Function?

You can identify a parent function by its shape and characteristics, such as the direction it shifts.

Why Is It Important To Know About Parent Functions?

Knowing about parent functions helps in understanding advanced topics in math like calculus.

What Are Some Examples Of Parent Functions?

Some examples of parent functions include linear, quadratic, cubic, absolute value, and exponential functions.

How Can You Use Parent Functions In Real Life?

Parent functions can be used in real life to model and analyze various phenomena, such as population growth and decay.

Conclusion

Parent functions are fundamental building blocks of functions and provide a framework for the significant types of functions in mathematics. They form the basis for the understanding of complex mathematical concepts, particularly in higher-level math classes. Hence a thorough comprehension of parent functions is crucial.

In this blog post, we took an in-depth look at what a parent function is, its importance, and the most commonly used parent functions, including linear, quadratic, cubic, reciprocal, and radical functions. We also provided examples and graphs that helped elucidate these concepts.

Acquiring a solid foundation in parent functions prepares students to tackle more complex functions, and also enables them to gain a deeper understanding of the concept of functions in general. Mastering parent functions is an integral part of succeeding in mathematics, and it is a skill that is well worth the effort to learn.

What Is A Parent Function?